About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsDerivative of tan^2x full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \geThe derivative of tan ( u) tan ( u) with respect to u u is sec 2 ( u) sec 2 ( u) Replace all occurrences of u u with 2 x − x 3 2 x x 3 Differentiate Tap for more steps By the Sum Rule, the derivative of 2 x − x 3 2 x x 3 with respect to x x is d d x 2 x d d x − x 3 d d x 2 x d d x2909 Using the chain rule, the derivative of tan^2x is 2tan(x)sec 2 (x) Finally, just a note on syntax and

Differentiate The Following By Using First Principle I Tan 2x 1 Ii Tan X Iii Maths Limits And Derivatives Meritnation Com
Derivative of tan^2(x^3)
Derivative of tan^2(x^3)- Find the derivative of tan (2x3) Get the answers you need, now!Find the derivative of the following w r t x by using method of first principle tan (2x 3) Mathematics and Statistics



Derivatives Of Inverse Trigonometric Functions
The formula for the derivative of cx, where c is a constant, is given in the following image Since the derivative of cx is c, it follows that the derivative of 2x is 2 What is the derivative of 1 3x?If you are new to chain rule, I would suggest you create new variables (in your head once you become good at it So here they are $$ u = 2x^4\\ v= \tan^{1} u \\ y=\ln v $$ to get $$ y = \ln(\tan^{1}(2 x^4)$$ Find the derivative of \(f(x)=2\tan x −3\cot x \) Hint Use the rule for differentiating a constant multiple and the rule for differentiating a difference of two functions\(f′(x)=2\sec^2 x3\csc^2
Solution For Find the derivative of tan (2x 3) HOME BECOME A TUTOR BLOG CBSE QUESTION BANK PDFs MICRO CLASS DOWNLOAD APP Class 12 Math Calculus Continuity and Differentiability 550 150 Find the derivative of tan (2 x 3) 550 150 Connecting you to a tutor in 60 seconds Get answers The Second Derivative Of tan (3x) To calculate the second derivative of a function, you just differentiate the first derivative From above, we found that the first derivative of tan (3x) = 3sec 2 (3x) So to find the second derivative of tan (3x), we just need to differentiate 3sec 2Y=tanh^3 (2x) * u=2x → du = 2dx * * y=tanh^3 (u) * * z=tanu → dz= 1 (tan u)^2 du * y=z^3 →dy = 3z^2 dz dy = 3z^2 dz dy = 3(tanu )^2 dz dy = 3(tanu )^2 *(1
To apply the Chain Rule, set u u as tan ( x) tan ( x) Differentiate using the Power Rule which states that d d u u n d d u u n is n u n − 1 n u n 1 where n = 3 n = 3 Replace all occurrences of u u with tan ( x) tan ( x) The derivative of tan(x) tan ( x) with respect to x x is sec2(x) sec 2 ( x) Reorder the factors of 3tan2(x)sec23 Write tanx/sinx as tan(x)/sin(x) 4 Use inv to specify inverse and ln to specify natural log respectively Eg1 Write sin1 x as asin(x) 2 Write ln Derivative is the important tool in calculus to find an infinitesimal rate of change of a function with respect to its one of the independent variableDerivative of 3tan(x) (3*tan(x))' (3)'*tan(x)3*(tan(x))' 0*tan(x)3*(tan(x))' 0*tan(x)3*(1/((cos(x))^2)) 3/((cos(x))^2) The calculation above is a derivative of the function f (x)



What Is The Nth Derivative Of Tan 1 X Quora
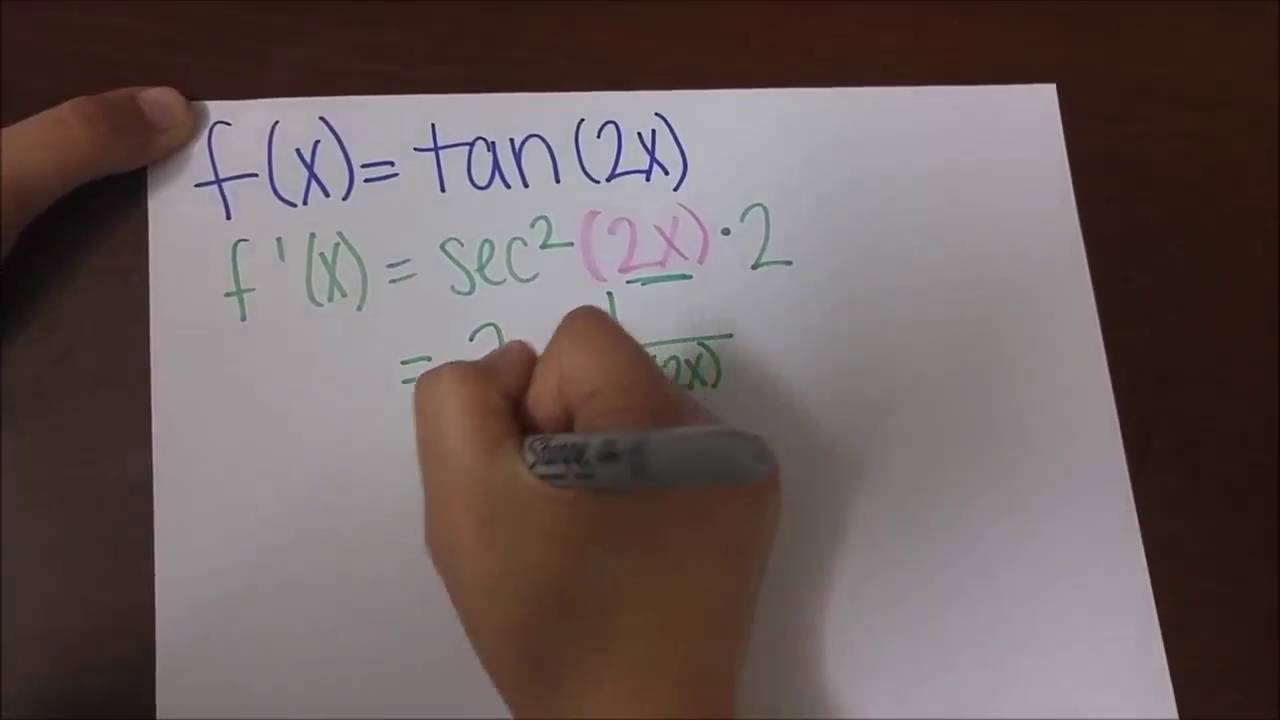



Ii F Find Derivative Of Tan 2x At X Pi 6 Youtube
The derivative of sin x is cos x,The derivative of cos x is −sin x (note the negative sign!) andThe derivative of tan x is sec2x, Now, if u = f(x) is a function of x, then by using the chain rule, we have`(d(sin u))/(dx)=cos u(du)/(dx)``(d(cos u))/dx=sin u(du)/(dx)``(d(tan u))/(dx)=sec^2u(du)/(dx)`Example 1Differentiate `y = sin(x^2 3)` Using the chain rule, the derivative of tan^2x is 2tan(x)sec 2 (x) Finally, just a note on syntax and notationtan^2x is sometimes written in the forms below (with the derivative as per the calculations above) Let y = tan (2x 3) We need to find derivative of y, ie 𝑑𝑦/𝑑𝑥 = (𝑑 tan〖(2𝑥3)〗)/𝑑𝑥 = sec2(2x 3) × (𝑑(2𝑥 3))/𝑑𝑥 = sec2 (2x 3) × 2 = 2 sec2 (2x 3) (As (tan x)' = sec2 x)




Derivative Of Inverse Tangent Video Khan Academy




Derivative Of Tan X Old Video Khan Academy
We can use the Chain Rule to "open" the derivative of this function deriving each one as it is and multiply together y' = 2sin2−1(2x 3)cos(2x 3) ⋅ (2) = = 4sin(2x 3)cos(2x 3) = 3 The instructions Use the definition of derivative to find f ′ ( x) if f ( x) = tan 2 ( x) I've been working on this problem, trying every way I can think of At first I tried this method lim h → 0 tan 2 ( x h) − tan 2Hi !!Solution Let f(x) = tan(2x3) , u(x) = 2x 3 = tan(2x3) = f(x) Thus, F is a composite of two function put t = u(x) = 2x 3 , then dvldt = sec²t dt/dx = RJRishabh RJRishabh Math Secondary School answered *Find the derivative of tan(2x3) * 2 See




How Do You Evaluate The Integral 1 Tan X 3 Sec 2 X Dx Within The Range 0 Pi 4 Socratic




Solving The Differential Equation Dy Dx Tan 2 X Y Youtube
Derivative of \(tanx = sec^2x \) What Is The Derivative Of tan(x)? The derivative of `f(x)=tan(2x pi/2)` is `f'(x) = 2*sec^2(2x pi/2)` and at `x = 3*pi/4` the slope of the tangent is 2 Approved by eNotes Editorial Team Luca B\( \frac{d}{dx} {tanx} = \frac{d}{dx} \frac{sinx}{cosx}\) we know that \( tanx =\frac{sinx}{cosx




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11




Derivatives Of Trigonometric Functions Ppt Download
The integration of uv formula is a special rule of integration by parts= —J x 2X1/21 —l x 6x1/3 01 1 o The derivative of a constant = Note The line y = 7 is a horizontal line Its slope is 0 Therefore its derivative (also its slope) equals 0 In other words, the derivative of a constant always equals zero Sum or Difference The derivative of tan 2x is 2 sec2 (2x) What is the differentiation of 0?




Brandi S Buzzar Blog Proof Derivative Tan X Sec 2 X



Derivatives Of Inverse Trigonometric Functions
The derivative of tan−1x is 1 1 x2 (for "why", see note below) So, applying the chain rule, we get d dx (tan−1u) = 1 1 u2 ⋅ du dx In this question u = 2x, so we get d dx (tan−12x) = 1 1 (2x)2 ⋅ d dx (2x) = 2 1 4x2Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs of the function and its derivatives Calculator supports derivatives up toShare It On Facebook Twitter Email 1 Answer 1 vote answered by Reyansh (191k points) selected by faiz Best answer Let f(x) = tan




Tan2x ただの悪魔の画像




Differentiate The Following From First Principle Tan2x Youtube
The derivative of tan (2x) is equal to two times the secant squared of two times x Using mathematical notation, the equation is written as d/dx tan (2x) = 2sec^2 (2x) The derivative of tan (2x) can be found by using the quotient rule and the chain rule Using the quotient rule, the tangent of 2x can be simplified to read the cosine squared ofDerivative of (12x^3^4) \tan \cot \sec \csc \sinh \cosh \tanh \coth \sech \arcsin \arccos \arctan \arccot \arcsec \arccsc \arcsinh (12x^{3}\right)^{4}\right) he Related Symbolab blog posts Advanced Math Solutions – Derivative Calculator, Implicit Differentiation We've covered methods and rules to differentiate functions of theSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Evaluate Limit X Tends To Pi 2 Tan 2x X Pi 2 Evaluate Sin X Sin A X A Maths Limits And Derivatives Meritnation Com




Math 1a Ucb Spring 10
Share It On Facebook Twitter Email 1 Answer 1 vote answered by PritiKumari (491k points) selected by Ruksar03 Best answer Let y = tan (2xSince 13 is constant with respect to x , the derivative of 13x 1 3 x with respect to x is 13ddxx 1 3 d d x x 1 Answer Gió Here you can distinguish three functions ()2 then sin and finally 2x 3;




Differentiate Tanx Tan 2x Tan 3x Tan 4x W R T X




The Derivative Of Tan 2x Derivativeit
Examples \frac {d} {dx} (\frac {3x9} {2x}) \frac {d^2} {dx^2} (\frac {3x9} {2x}) (\sin^2 (\theta))'' derivative\of\f (x)=34x^2,\\x=5 implicit\derivative\\frac {dy} {dx},\ (xy)^2=xy1Click here👆to get an answer to your question ️ Find the derivative of following functions wrt x tan (2x 3)Derivative of ln (2x^3)*tan (2x) Simple step by step solution, to learn Simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving process




Derivative Rules For Trigonometric Functions




Differentiate The Following By Using First Principle I Tan 2x 1 Ii Tan X Iii Maths Limits And Derivatives Meritnation Com
Find the derivative of the function tan (2x 3) from the definition (first principles) class12;Derivative of tan 2x 3 by first principleFind the derivative of #cscx# from first principles?Feb , 16 Limits and Derivatives differentation of tan3x by first principle Share with your friends Share 0 Dear Student, Please find below the solution to the asked query We have f x = tan 3 x f xGraph of tan x and its Derivative The graphs of \( \tan(x) \) and its derivative are shown below Derivative of the Composite Function tan (u(x)) We now have a composite function which is a function (tan) of another function (u)




What Is The Derivative Of Tan 3theta With Respect To Sec 3theta At Theta P 3 Quora




Q42 Differentiate Tan 2x 3 Derivative Of Tan 2x 3 Differentiation Of Tan 2x 3 Youtube
What is UV formula? Find the derivative of following functions wrt x tan (2x 3) differentiation;By the Sum Rule, the derivative of with respect to is Since is constant with respect to , the derivative of with respect to is Differentiate using the Power Rule which states that is where



Derivatives Of Trigonometric Functions Web Formulas




Ex 7 2 21 Integrate Tan2 2x 3 Class 12 Cbse Ex 7 2
1 Log in Join now 1 Log in Join now Ask your question Brainly User Brainly User Math Secondary School Find the derivative of tan (2x3) 2Derivative of tan(2x3) using first principle Let's find the derivative of tan x 2 Step 1 Identify g ( x) g ( x )= x 2 Step 2 Find g' ( x) g' ( x) = 2 x Step 3 Use the Chain Rule Other Ways to Write the Solution Since the reciprocal




Differentiation With Trig Outcomes Ppt Download
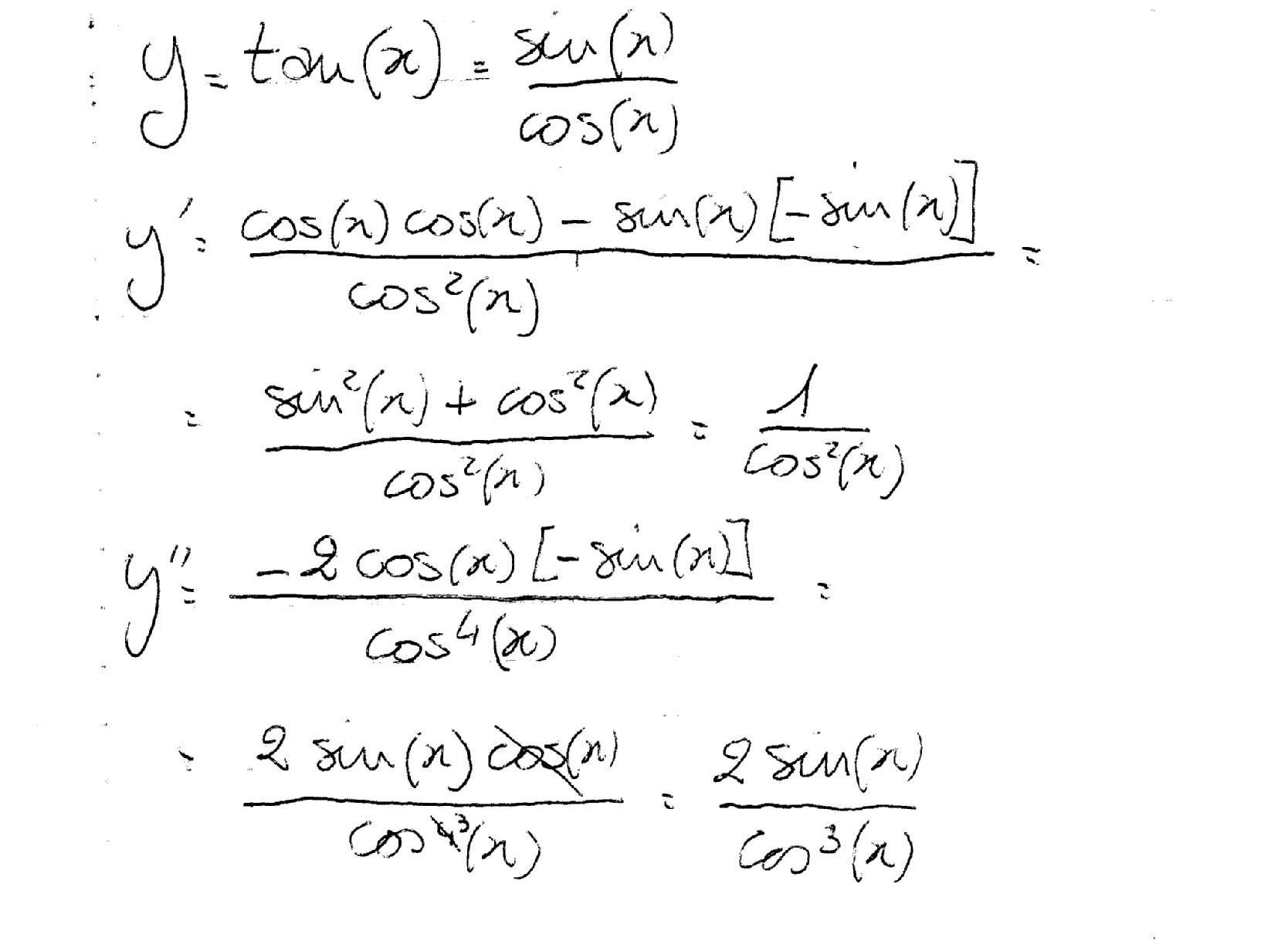



What Is The 2nd Derivative Of Y Tanx Socratic
From the derivative of \sin(x), \cos(x) and \tan(x) can be determined \cos(x) can be found by using the chain rule and the identity \cos(x)=\sin(x90) \tan(x) can then be found by the quotient rule and the identity \tan(x)=\frac{\sin(x)}{\cos(x)}Given a function , there are many ways to denote the derivative of with respect to The most common ways are and When a derivative is taken times, the notation or is used These are called higherorder derivatives Note for secondorder derivatives, the notation is often used At a point , the derivative is defined to beSolutionShow Solution Let `y = tan^ (1) ( (5x 1)/ (3x6x^2))` `= tan^ (1) ( (5x1)/ (12x6x^2))` `= tan^ (1) ( (5x 1)/ (1 (3x 2) (2x11)))` `= tan^ (1) ( ( (3x2) (2x1))/ ( (1 (3x2)) (2x1)))` `y = tan^ (1) (3x 2) tan^ (1) (2x 1)` Differentiate wrt x




Prove That Derivative Of Tan X Is Sec 2 X By First Principle




What Is The Derivative Of Tan 2x Socratic
Approximating a Value of \(4^π\) We also assume that for \(B(x)=b^x,\, b>0\), the value \(B′(0)\) of the derivative exists In this section, we show that by making this one additional assumption, it is possible to prove that the function \(B(x)\) is differentiable everywhereThe Derivative Calculator will show you a graphical version of your input while you type Make sure that it shows exactly what you want Use parentheses, if necessary, e g " a/ (bc) " In " Examples", you can see which functions are supported by the Derivative Calculator and how to use themThe derivative of 0 is 0 READ What do I need to know before babysitting?



1




3 Determine The First Derivative Of The Following Gauthmath
The derivative of tan 2x is 2 sec 2 (2x) (ie) d/dx tan 2x = 2 sec 2 (2x) Explanation We know that the derivative of tan x is sec 2 x (ie) d/dx (tan x) = sec 2 x According to the chain rule, d/dx tan 2x = sec 2 (2x) d/dx (2x) Therefore, d/dx tan 2x = 2 sec 2 (2x)Solution For Find the derivative of tan (2x 3) DOWNLOAD APP MICRO CLASS PDFs CBSE QUESTION BANK BLOG BECOME A TUTOR HOME HOME BECOME A TUTOR BLOG CBSE QUESTION BANK PDFs MICRO CLASS DOWNLOAD APP Class 12 Math Calculus Continuity And Differentiability 540 150 Find the derivative of tan (2 x 3)Derivative of tan(2x3) using first principle Answers 3 Get \ Other questions on the subject Mathematics Mathematics, 2300, neariah24




Second Derivative Of Tan 2x Youtube




The Derivative Of Tan X Is Sec 2 X Why Mathematics Stack Exchange




Derivative Of Tan 2x 3 Is A 2sec 2x 3 B Sec 2x 3 C Sec 2x 3 D None Of These Snapsolve




What Is The Nth Derivative Of Arctan 2x 1 X 2 In Terms Of R And Theta Quora



Www Math Purdue Edu Kyochman Ma Lesson14 Notes Implicitdifferentiation Pdf



1 Derivatives Of Sine Cosine And Tangent




If Y 3 Log9 1 Tan 2x Then Dydx




Find Second Order Derivative Of X 3 Tanx




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x




Example 22 Find Derivative Of Tan 2x 3 Chapter 5 Class 12




Me 21 If Fx X5 Sin 2x Tan 2x Cos 3x Then Deriv Gauthmath




Find Derivative Of Xsin2x 5 X K X Tan 2x 3 Q 13 X Sin 2x 5x Kx Tan2x3 Maths Limits And Derivatives Meritnation Com



1




Find The First And The Second Order Partial Chegg Com




Weierstrass Substitution Wikipedia



2




Derivative Of Tan 2x 3




Prove That Derivative Of Tan X Is Sec 2 X By First Principle




Let F X Tan2x Tan3x Tan5x Then F Pi Equals




Derivative Of Tan 2x 3 From First Principle Brainly In
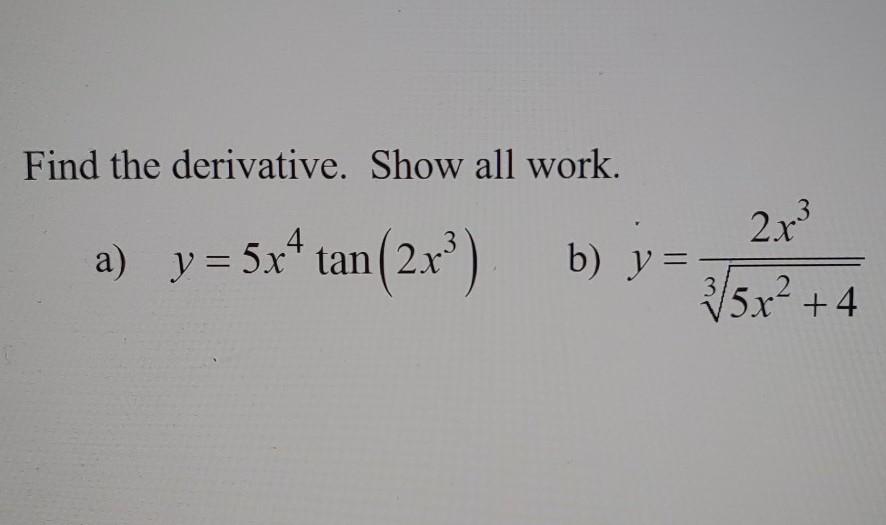



Find The Derivative Show All Work 2x3 A Y 5x4 Chegg Com



Www Math Purdue Edu Kyochman Ma Lesson14 Notes Implicitdifferentiation Pdf




Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3
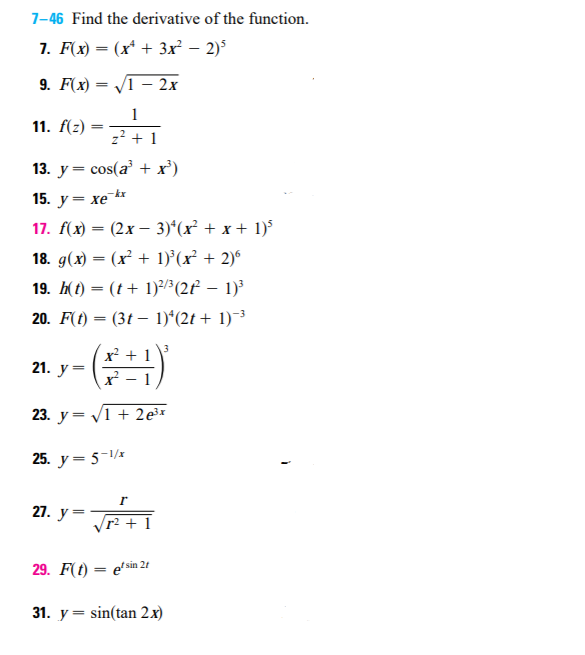



7 46 Find The Derivative Of The Function 13 Chegg Com



Differentiate Sin Tan 1 2x W R T X And Express The Result Free From Trigonometric Symbols From Mathematics Continuity And Differentiability Class 12 Cbse



How To Prove That The Derivative Of Tan X Is Sec 2 X Quora



Differentiating Trigonometric Functions Review Article Khan Academy



Derivative Of Tan X




1 Find The Derivative Of Each Function A E E 7 Chegg Com



2
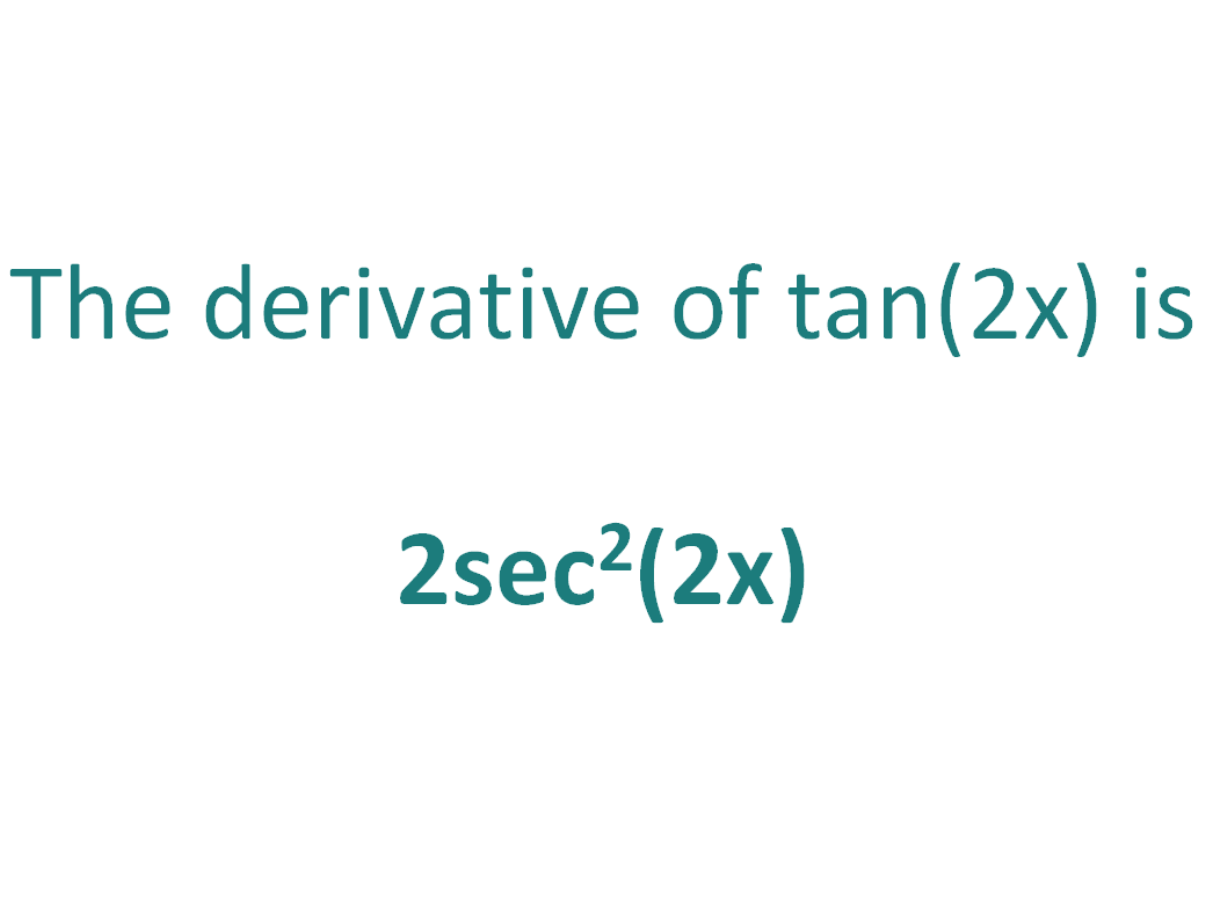



The Derivative Of Tan 2x Derivativeit




Find The Derivative Of Tan 2x 3 Brainly In




Derivative Of Arctan X Inverse Tangent Detailed Lesson




Find The Derivative Of Tan 2x 3 Youtube




Tan2x ただの悪魔の画像



Differentiate The Following From First Principles I Tan 2 X Ii Tan 2x 1 Sarthaks Econnect Largest Online Education Community




Find The Derivative Of Tanx By First Principle Mathematics Topperlearning Com Iyyne




05 Derivative Of Tangent Function Tan2x And Tanx 2 Youtube



Derivatives Of Trigonometric Functions




Find The Derivative Of Y Tan 3 2x Youtube




1 Use The Chain Rule To Find The Derivative Of F X Chegg Com




Find The Derivative Of Each Function 1 Y Tan 3x 4 Chegg Com
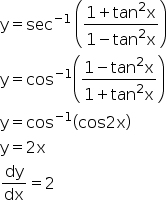



Differentiate Wrt X Sec 1 1 Tan2x 1 Tan2x Mathematics Topperlearning Com Nti7rxx




How To Take The Derivative Of Tan X Video Lesson Transcript Study Com



3




Derivative Of Tan X Proof In Easy Steps Calculus How To




What Is The Derivative Of Tan 2x



If T Tan X What Is Tan2x The Student Room




Question 1 Integrate The Following Function Sec 2x Chegg Com




Derivative Of Arctan X Inverse Tangent Detailed Lesson




Differentiation Of Tan 2 X And X 3 X 4 Youtube




How To Take The Derivative Of Tan X Video Lesson Transcript Study Com
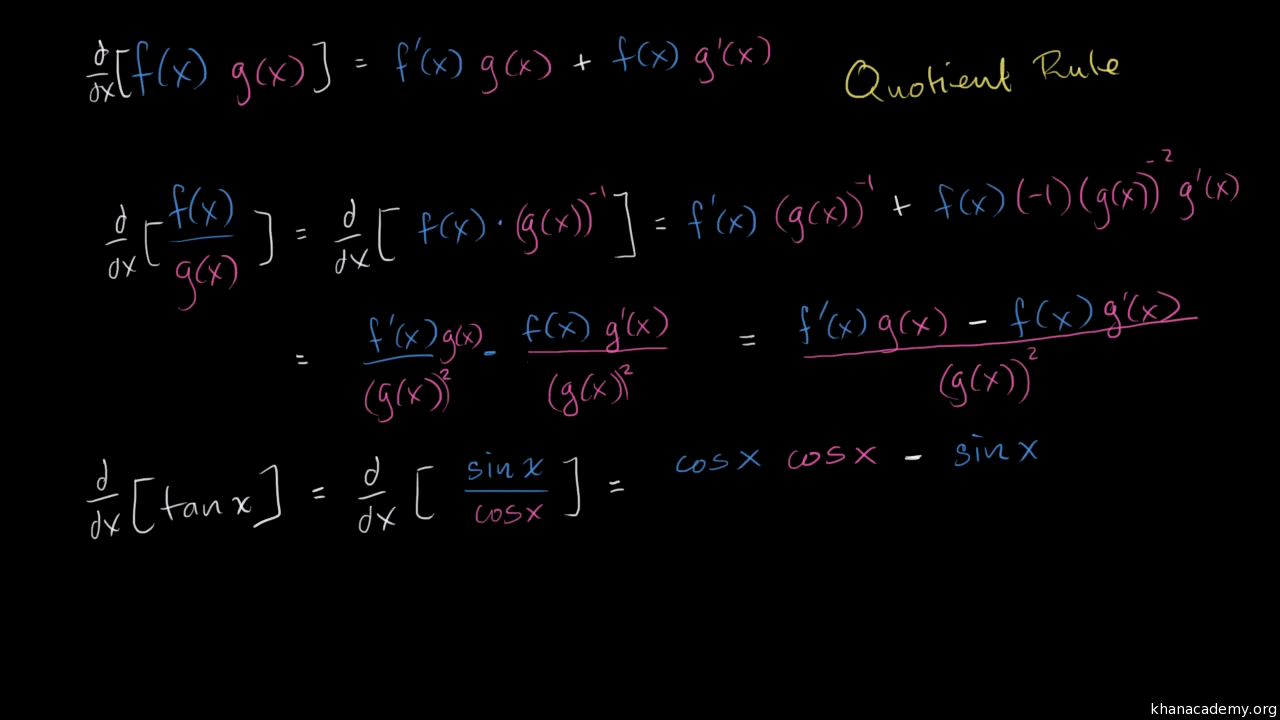



Derivative Of Tan X Old Video Khan Academy
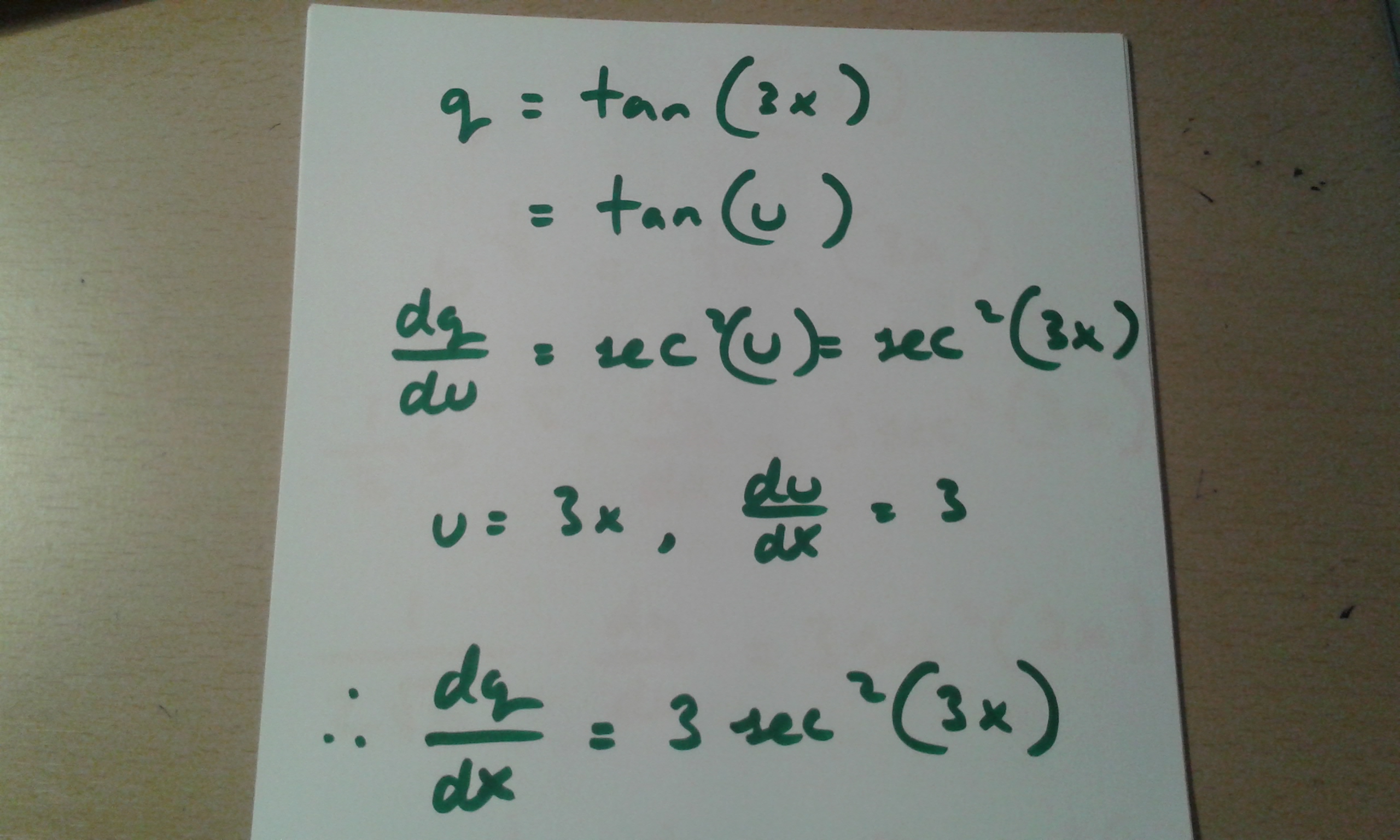



How Do You Find The Derivative Of Tan 2 3x Socratic




Differentiate The Following From First Principle Tan 2x 1



What Is D Dx Tan2x Quora
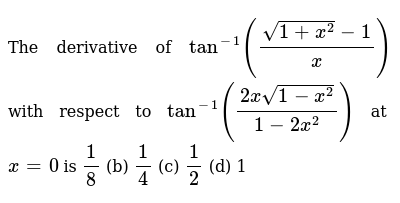



The Derivative Of Tan 1 Sqrt 1 X 2 1 X With Respect To Tan 1 2xsqrt 1 X 2 1 2x 2 At X 0 Is 1 8 B 1 4 C 1 2 D 1




How To Take The Derivative Of Tan X Video Lesson Transcript Study Com



Find The Derivative Of The Function Tan 2x 3 From The Definition First Principles Sarthaks Econnect Largest Online Education Community
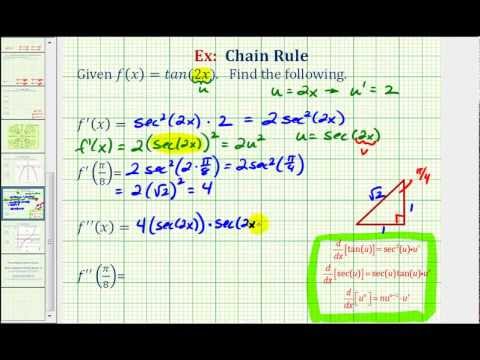



Ex 1 First And Second Derivatives Using The Chain Rule F X Tan 2x Youtube



1




Find The Derivative Of Tan 2x 3 Brainly In




Tan2 Derivative ただの悪魔の画像
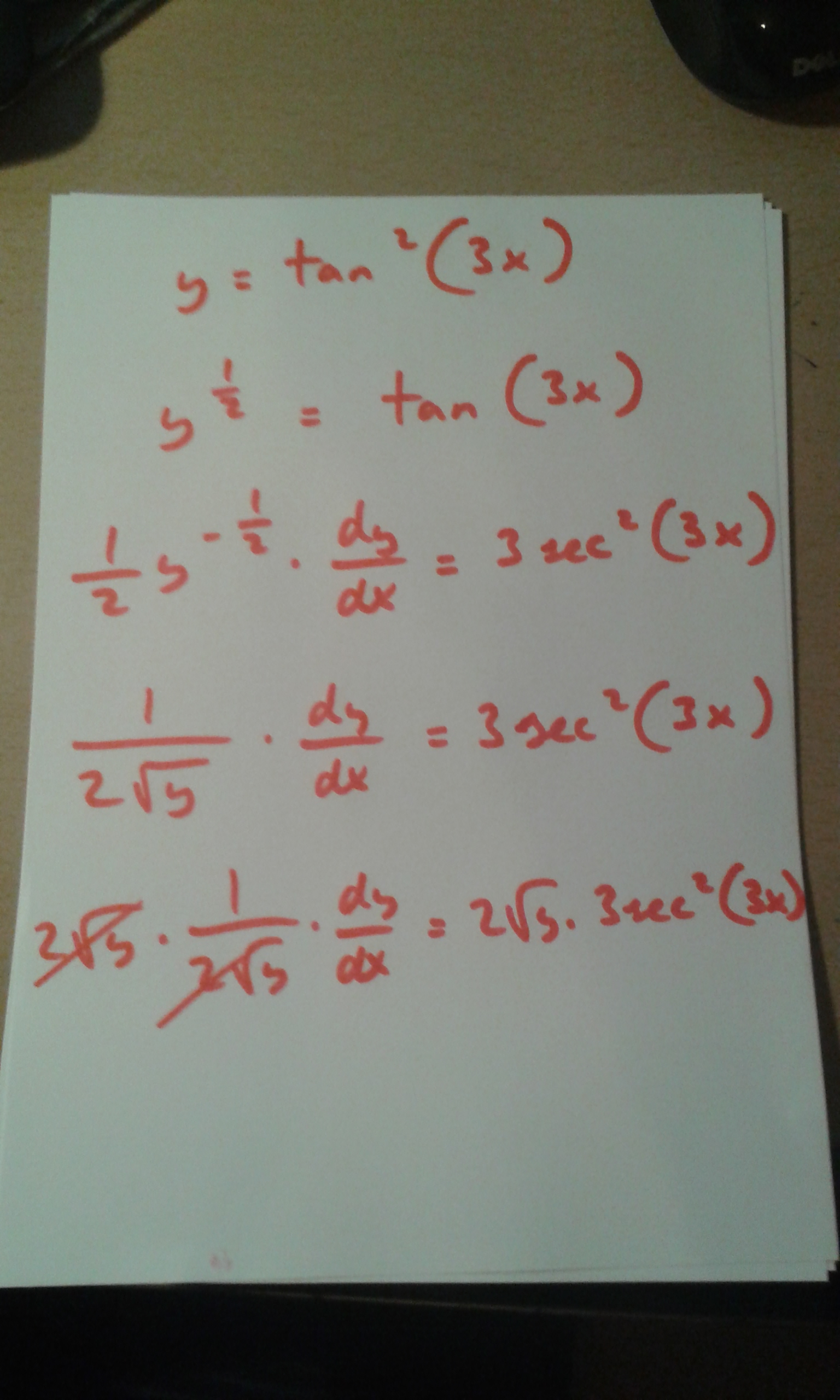



How Do You Find The Derivative Of Tan 2 3x Socratic
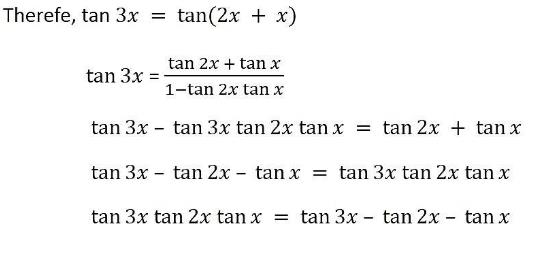



Prove That The Differentiation Of Tan3x Tan2x Tanx Is 3sec 3x 2sec 2x Sec X Edurev Class 12 Question
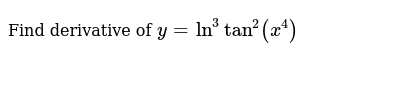



Find The Derivative Of Tan 2x 3




Differentiate Y 1 Sec X Tan X Sec X 1 Sec X Tan 2 Chegg Com



What Is Math Int Tan 2 2x Dx Math Quora




Differentiation Of Tanx 2 Youtube




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange




Find The Derivative 23 Y Tanx 2 3 Aj Dy 2 3 Sec X Chegg Com




How To Take The Derivative Of Tan X Video Lesson Transcript Study Com




A Differentiate The Following Function With Respect Chegg Com
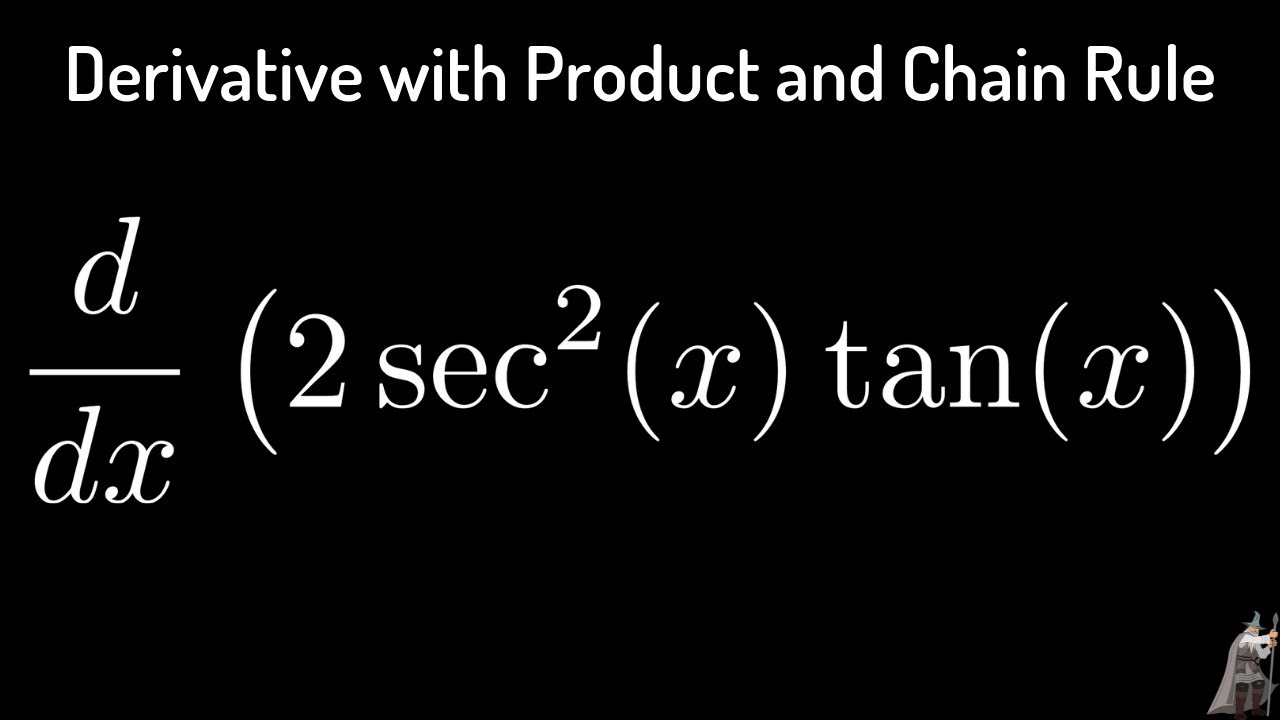



The Derivative Of H X 2 Sec 2 X Tan X Product Rule Example Youtube




Evaluate The Given Limit Lim X Pi 2 Tan 2x X Pi 2 Mathematics Shaalaa Com


